Volume
Introduction to VolumeIn a previous lesson you learned about area, which is a measurement of the amount of space in a two-dimensional shape. In this lesson you will learn about volume, which is a measurement of the amount of space in a three-dimensional figure, such as a shoebox or a cube.
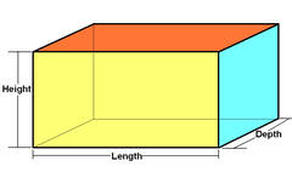
Take a look at this three-dimensional box. It is actually called a rectangular prism, but you can think of it as a shoebox or a suitcase. Very often in math, we need to find the volume of a three-dimensional figure. That means we want to know how much space is inside it. For example, we may want to know how much we can pack inside a suitcase.
In a two-dimensional rectangle, we saw dimensions of length and width. In a 3-Dbox like this, we need to add an extra dimension. It is called depth, or sometimes height. All that really matters is that we have measurements for each dimension.
For a box like the one shown, the formula for volume is: V = L x W x D. Volume equals length times width times depth. We just multiply all of the dimensions. For example, if a box has dimensions of 2 cm, 3 cm , and 4 cm, the volume is 24, but we can't leave the answer like that.
Remember that when we calculated area, we had to state that the answer was in "units squared." That's because the area really measures how many unit squares can fit inside the shape. Here we're actually measuring how many unit cubes can fit inside the shape. So we have to write our answer as 24 cm3, which is read as "twenty-four cubic centimeters," or "twenty-four centimeters cubed."
Take a look at this three-dimensional box. It is actually called a rectangular prism, but you can think of it as a shoebox or a suitcase. Very often in math, we need to find the volume of a three-dimensional figure. That means we want to know how much space is inside it. For example, we may want to know how much we can pack inside a suitcase.
In a two-dimensional rectangle, we saw dimensions of length and width. In a 3-Dbox like this, we need to add an extra dimension. It is called depth, or sometimes height. All that really matters is that we have measurements for each dimension.
For a box like the one shown, the formula for volume is: V = L x W x D. Volume equals length times width times depth. We just multiply all of the dimensions. For example, if a box has dimensions of 2 cm, 3 cm , and 4 cm, the volume is 24, but we can't leave the answer like that.
Remember that when we calculated area, we had to state that the answer was in "units squared." That's because the area really measures how many unit squares can fit inside the shape. Here we're actually measuring how many unit cubes can fit inside the shape. So we have to write our answer as 24 cm3, which is read as "twenty-four cubic centimeters," or "twenty-four centimeters cubed."

