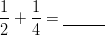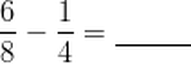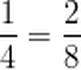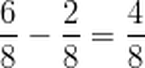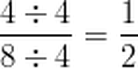- Adding and Subtracting fractions with unlike Denominator.
READ: Add Fractions With Different Denominators
Add Fractions With Different Denominators
Not all fractions have common or like denominators. When we have fractions with unlike denominators, we can still add them, but we will need to rename the fractions before we can add them. How do we add fractions with different denominators?
To add fractions that have different denominators, we have to rename the fractions so that they are alike. We rename them by changing the different denominators of the fractions to like denominators.
For Ex.
Add Fractions With Different Denominators
Not all fractions have common or like denominators. When we have fractions with unlike denominators, we can still add them, but we will need to rename the fractions before we can add them. How do we add fractions with different denominators?
To add fractions that have different denominators, we have to rename the fractions so that they are alike. We rename them by changing the different denominators of the fractions to like denominators.
For Ex.
In this example, we are trying to add halves and fourths. If something is divided into halves, it is divided into two pieces. If something is divided into fourths, it is divided into four pieces. We are trying to add fourths and halves. They are different quantities. You can see that although the bar is the same size, the parts are different sizes. We have to rewrite these fractions so that they have common denominators.
How do we rewrite fractions to have a common denominator?
The first step in doing this is to the find the least common multiple of both of the denominators. This LCM will become the lowest common denominator.
Let’s look at 2 and 4.
First, name the multiples of 2: 2, 4, 6, 8, 10 . . . .
Next, name the multiples of 4: 4, 8, 12, 16
The least common multiple of 2 and 4 is 4.
Our next step is to rewrite each fraction as an equivalent fraction that has four as a denominator.
1/2 = /4 to name one-half in terms of fourths, we need to multiply the numerator and denominator by the same number. 2 2 4, so we multiply the numerator by 2 also. 1* 2 * = 2.
Our second fraction 1/4 is already written in terms of fourths so we don’t need to change it at all.
2/4 + 1/4 = 3/4
Next, we can add the renamed fractions.
Our answer is .3/4 This answer is in simplest form, so our work is complete.
As long as you rename fractions with the lowest common denominator, you can add any number of fractions with unlike denominators.
The first step in doing this is to the find the least common multiple of both of the denominators. This LCM will become the lowest common denominator.
Let’s look at 2 and 4.
First, name the multiples of 2: 2, 4, 6, 8, 10 . . . .
Next, name the multiples of 4: 4, 8, 12, 16
The least common multiple of 2 and 4 is 4.
Our next step is to rewrite each fraction as an equivalent fraction that has four as a denominator.
1/2 = /4 to name one-half in terms of fourths, we need to multiply the numerator and denominator by the same number. 2 2 4, so we multiply the numerator by 2 also. 1* 2 * = 2.
Our second fraction 1/4 is already written in terms of fourths so we don’t need to change it at all.
2/4 + 1/4 = 3/4
Next, we can add the renamed fractions.
Our answer is .3/4 This answer is in simplest form, so our work is complete.
As long as you rename fractions with the lowest common denominator, you can add any number of fractions with unlike denominators.
Subtract Fractions with Different Denominators
Just as we can add fractions with different denominators by renaming them with the lowest common denominator, we can also subtract fractions with different denominators by doing the same thing.
First, remember that to subtract two fractions with different denominators, we have to make them fractions with the same denominator. We do this by finding the least common multiple and then we rename each fraction as an equivalent fraction with that least common multiple as the lowest common denominator.
Example
Just as we can add fractions with different denominators by renaming them with the lowest common denominator, we can also subtract fractions with different denominators by doing the same thing.
First, remember that to subtract two fractions with different denominators, we have to make them fractions with the same denominator. We do this by finding the least common multiple and then we rename each fraction as an equivalent fraction with that least common multiple as the lowest common denominator.
Example
First, find the least common multiple of 4 and 8. It is 8.
Next, rename each fraction in terms of eighths. Remember that renaming is another way of saying that we create an equivalent fraction in terms of eighths.
6/8 is already in terms of eighths. We leave it alone.
Next, rename each fraction in terms of eighths. Remember that renaming is another way of saying that we create an equivalent fraction in terms of eighths.
6/8 is already in terms of eighths. We leave it alone.
Now we can rewrite the problem and find the difference.
We can simplify four-eighths by dividing the numerator and the denominator by the GCF. The GCF is 4.